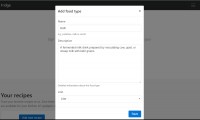
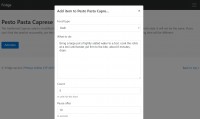
Tag: CTF
Соревнования по компьютерной безопасности Capture The Flag







Год назад мы играли в Google CTF. В этом году решили не отставать и снова размяться командой старичков
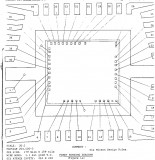
Это заметка о том, как мы с Костей Плотниковым решали задание на ассиметричную криптографию с Google CTF, который прошёл неделю назад