«У слова тон значений больше, чем снега в горах.»
Иоанн де Грокейо

Привет! Сегодня мы поговорим про ноты. Да-да, те самые, которые до-ре-ми-фа-соль-ля-си. Почему в этом ряду их всегда семь? Почему после си снова идёт до, но следующей октавы? И почему на фортепиано между этим семью белыми нотами есть ещё пять чёрных? Почему их ровно пять, и почему они так странно расположенны?

Удивительно, но ответы на эти вопросы вы скорее услышите на уроках физики и математики, чем в музыкальной школе.

Немножко физики

Давайте для начала возьмём обычную акустическую гитару как один из самых наглядных музыкальных инструментов — вы дёргаете за струну, она колеблется, вместе с ней колеблется воздух, и вы слышите ноту.

Высота услышанной ноты зависит от частоты колебаний струны, то есть от того, сколько колебаний она успевает сделать за одну секунду. Например, ля первой октавы — это 440 Гц, то есть ровно 440 колебаний в секунду. У низких нот частота меньше, а у высоких — больше.

В реальности чистого колебания с нужной частотой добиться практически невозможно. Вместо этого колебание струны представляет собой сумму сразу нескольких колебаний — всей струны, двух её половинок с частотой в два раза больше, трёх её третинок с частотой в три раза больше и так далее.

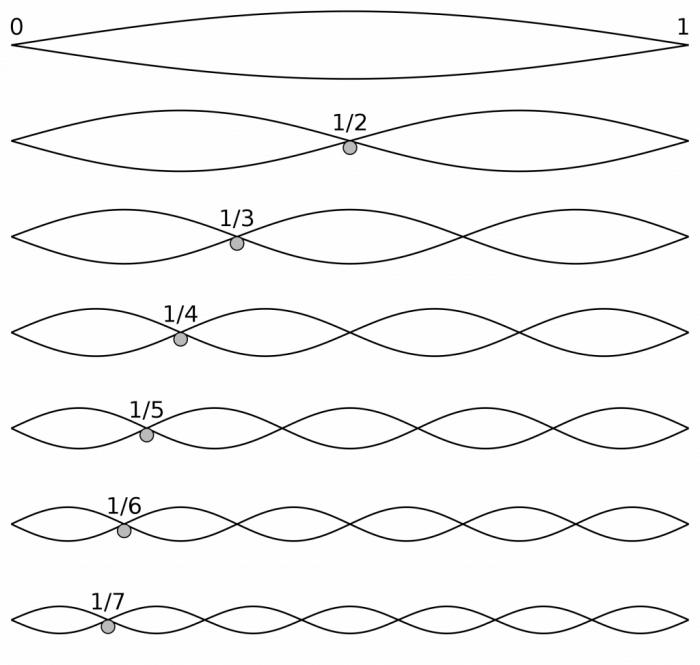
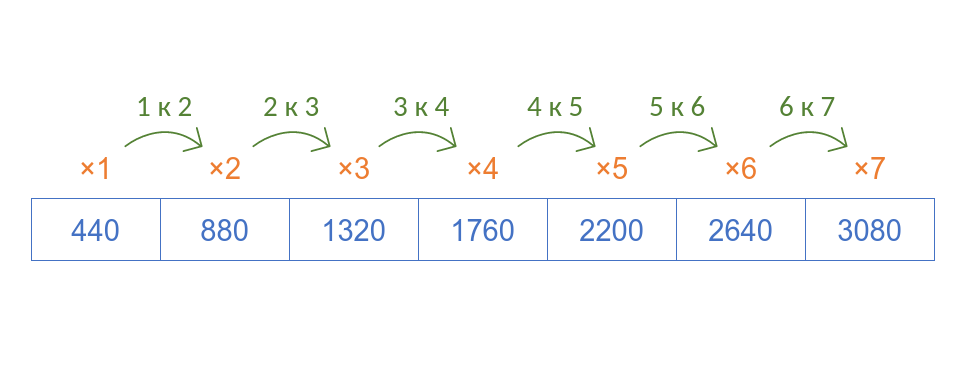
Музыканты в этот момент говорят, что звук, который вы слышите, образуется как сумма основного тона (например, ноты ля с частотой 440 Гц) и обертонов (от немецкого ober — высокий) — колебаний с частотой 880 Гц, 1320 Гц, 1760 Гц и так далее. Наше ухо воспринимает такую склейку позитивно, ведь все встречающиеся в природе звуки образуются ровно таким образом.

Здесь нам важно запомнить, что с точки зрения нашего уха колебания с частотами $\nu$, $2 \cdot \nu$, $3 \cdot \nu$, $4 \cdot \nu$ и так далее хорошо сочетаются друг с другом и приятно звучат. При этом частоты соседних колебаний относятся друг к другу как 1 к 2, 2 к 3, 3 к 4 и так далее. Благодаря этому факту появятся на свет приятные нашему слуху октавы, квинты, кварты и терции, но об этом чуть позже :-)

Отдельного внимания заслуживает первый обертон — тот самый, что имеет частоту в два раза больше, чем основной тон. Если взять его за основу и построить обертоны уже к нему, то этот ряд наполовину будет состоять из обертонов его старшего брата. Как следствие, итоговый звук зазвучит в нашем ухе очень похожим образом, хотя и выше.

Именно поэтому две получившиеся ноты (построенные от частоты $\nu$ с её обертонами и от частоты $2 \cdot \nu$ с её обертонами) решили называть одинаково — и там ля, и тут ля. А чтобы эти ля различать, придумали, собственно, октавы. Нота, построенная на основной частоте 440 Гц — это ля первой октавы, а на основной частоте 880 Гц — ля второй октавы. Ля третьей октавы построено уже на 1760 Гц, дальше идёт ля четвёртой октавы и так далее. Октавы ниже первой тоже существуют — ля малой октавы строится на 220 Гц, ля большой — на 110 Гц и так далее.

Немножко математики

Окей, с октавами разобрались. Но откуда берутся остальные ноты внутри октавы? На самом деле они появляются достаточно естественным образом. Мы только что выяснили, что обертоны для ля первой октавы звучат на частотах 880 Гц, 1320 Гц и 1760 Гц. Про 880 Гц и 1760 Гц нам уже всё понятно — это ля второй и третьей октавы. А вот что такое 1320 Гц? Если частоты нот ля второй и третьей октавы относятся друг к другу как 1 к 2, то частота этой лежащей между ними ноты соотносится с ними как 2 к 3 и 3 к 4 (а $\frac{2}{3} \times \frac{3}{4}$ как раз равно $\frac{1}{2}$ — радует, что математически мы ещё нигде не ошиблись). Эта промежуточная нота — нота ми. На самом деле это не совсем современная нота ми, но мы об этом поговорим позже. Пока давайте считать, что это честная ми, образующая квинту с ля второй октавы и кварту с ля третьей октавы. Названия «квинта» и «кварта» на самом деле появятся позже, но уже сейчас нам нужно как-то обозначать музыкальные интервалы (промежутки между двумя нотами), вот давайте и воспользуемся правильными названиями: интервал между нотами с соотношением основных частот 2 к 3 будем называть квинтой, а с соотношением 3 к 4 — квартой.

Получается, что обертоны располагаются следующим образом: первый — через октаву после базового тона, второй — через квинту после первого обертона и третий — через кварту после второго (что то же самое, что через две октавы после базового тона). Ну а дальше аналогично появляются и остальные интервалы — большая терция (интервал с соотношением частот 4 к 5) и малая терция (5 к 6). Чтобы можно было сыграть такие интервалы на наших инструментах, внутри октавы появляются и другие ноты.

Вот только незадача — у музыкантов и математиков никак не получалось выбрать конечное (и желательно небольшое, конечно) количество нот и расположить их внутри октавы так, чтобы любая пара нот давала один из приятных интервалов, описанных выше, или составлялся из нескольких таких. То там, то сям что-нибудь не клеилось.

Одной из первых успешных попыток решить эту задачу считают Пифагоров строй. Пифагор расположил семь нот внутри октавы со следующими соотношениями частот между парами соседних нот:

$$
\frac{8}{9} \hspace{4em} \frac{8}{9} \hspace{4em} \frac{243}{256} \hspace{4em} \frac{8}{9} \hspace{4em} \frac{8}{9} \hspace{4em} \frac{8}{9} \hspace{4em} \frac{243}{256}
$$

Обратите внимание — в этой последовательности встречается только два интервала — $\frac{8}{9}$, он побольше, и $\frac{243}{256}$, он поменьше (да, чем меньше число, тем больше интервал. Целая октава — это вообще $\frac{1}{2}$, как вы помните). Причём интервал $\frac{243}{256}$ встречается то через два больших интервала, то через три. Прямо как чёрные клавиши на фортепиано ;-)

Понятно, кстати, откуда здесь взялась дробь $\frac{8}{9}$ — это разность между двумя главными (после октавы, конечно) интервалами: квинтой и квартой.

$$\frac{2}{3} : \frac{3}{4} = \frac{8}{9}$$

В Пифагоровом строе не всё гладко — во-первых, эти двести-сорок-три двести-пятьдесят-шестых, которые появились как число, которого не хватало в ряду, чтобы произведение чисел во всём ряду было равно $\frac{1}{2}$. Смотрите: $\left(\frac{243}{256}\right)^2 \times \left(\frac{8}{9}\right)^5 = \frac{3^{5 \times 2}}{2^{8 \times 2}} \times \frac{2^{3 \times 5}}{3 ^ {2 \times 5}} = \frac{1}{2}$.

Во-вторых, фишкой пифагоровского строя было то, что от любой ноты можно было отложить не только октаву, но и чистую квинту, ведь $\frac{8}{9} \times \frac{8}{9} \times \frac{243}{256} \times \frac{8}{9} = \frac{1}{2}$. Исключение составляла только нота си, от неё квинта не откладывалась.

Пифагор попытался решить эту проблему добавлением в строй ещё пяти нот, тем самым разбив каждый из интервалов, равных $\frac{8}{9}$, на два более мелких интервала. С математической точки зрения он построил замыкание множества частот относительно операции откладывания квинты (то есть умножения и деления на $\frac{2}{3}$). Квинта от ля — это ми, квинта от ми — это си, но уже следующей октавы. Чтобы «вернуть» си в нашу октавы, просто делим частоту на два и продолжаем.

Немножко истории

Вы не поверите, но эта система просуществовала на протяжении 12 веков! Дольше, чем любая другая известная музыкальная система. Вот только музыкантов постоянно бесила так называемая волчья квинта. Дело в том, что если в системе Пифагора отложить квинту 12 раз, то мы должны получить исходную ноту, просто на 7 октав выше. Но на самом деле мы получим чуууть-чуть более высокую ноту, ведь $\left(\frac{3}{2}\right)^{12} \approx 129.746$, что чуть больше, чем $2^7=128$. Накопленную разницу называли пифагорейской коммой, и чтобы избавиться от неё, частоту какой-нибудь одной ноты немного подкручивали. В итоге одна из квинт внутри октавы получалась короче остальных и звучала абсолютно отвратительно, будто волки воют...

В итоге музыканты тех времён просто старались не играть смещённую ноту :-). Из-за этого было сложнее менять тональности у произведений, сложнее настраивать инструменты и тяжелее импровизировать. Неудивительно, что рано или поздно кто-то должен был придумать что-то ещё.

Этим кем-то стал Андреас Веркмейстер. Он сформулировал задачу так. Первое: нужно сохранить в октаве двенадцать традиционно устоявшихся звуков. Всё-таки 12 веков музыкальной истории так просто на помойку не выкинешь. Второе: никакой коммы быть не должно. И третье: все соотношения между соседними частотами должны быть абсолютно равными. Вот это было поистине революционное решение!

Математически Веркмейстер взял октаву с соотношением 1 к 2 и распределил её поровну между 12 нотами. Если две соседние ноты отличаются по своей частоте в $x$ раз, то $x^{12} = 2$, а значит, $x = \sqrt[^{12}]{2}$, вот и всё.

Частота ноты до-диез — это частота до, умноженная на $\sqrt[^{12}]{2}$. Частота ноты ре, следующей после до-диеза, это частота до-диеза, умноженная ещё на $\sqrt[^{12}]{2}$. И так далее! Через 12 нот получается идеальная октава.

Такие образом, Веркмейстер по сути равномерно распределил Пифагорову комму между всеми звуками внутри каждой октавы. Комма рассосалась и стала незаметной. Но досталось это счастье большой ценой: внутри октавы не осталось ни одного чистого интервала. Даже квинта — интервал, тысячелетиями считавшийся незыблемым — стала чуть короче, теперь она равна не $\frac{2}{3}$, а $\frac{1}{\sqrt[^{12}]{2}^7}$, то есть примерно $0,66742$.

Многих музыкантов поначалу возмутило предложение Веркмейстера. Однако через 30 лет почти все смирились с компромиссом, потому что разница между чистой настройкой и той, что предложил Веркмейстер, была едва уловимой, а достоинства нового строя постепенно стали очевидными. Исчезла волчья квинта. Стало возможным переходить из тональности в тональность и из мажора в минор как угодно. В ладу (например, в до-мажоре) остались те же семь основных звуков, но теперь лад мог начинаться с любой клавиши, хоть с белой, хоть с черной. Впервые делом доказал это великий Бах, написав цикл произведений для всех двадцати четырех тональностей — двенадцати минорных и двенадцати мажорных. До реформы Веркмейстера такое количество тональностей существовало лишь теоретически, а на практике было невыполнимо, ибо пришлось бы чуть не для каждой из них заново перестраивать инструмент.

Вместо заключения

Зачем я вам всё это рассказал? Во-первых, это красиво :-)

Во-вторых, я сейчас всё чаще понимаю, почему раньше существовали только доктора философии вместо современных докторов музыки или докторов математических и физических наук. Смог бы человек без понимания математики или физики придумать ноты? И, может, стоит нашим детям давать побольше кросс-предметных тем, чтобы они понимали, что ни математика, ни музыка, ни любые другие науки не существуют изолированно, друг без друга?

Бонус!

Первая струна классически настроенной гитары — это ми первой октавы. После этого поста, надеюсь, вы знаете, насколько легко сыграть на гитаре другое ми — ми второй октавы. Достаточно просто пережать первую струну посередине и дёрнуть за неё. Длина колеблющейся струны уменьшится в два раза, частота колебаний от этого увеличится в два раза, а, значит, нота перенесётся ровно на октаву вверх.